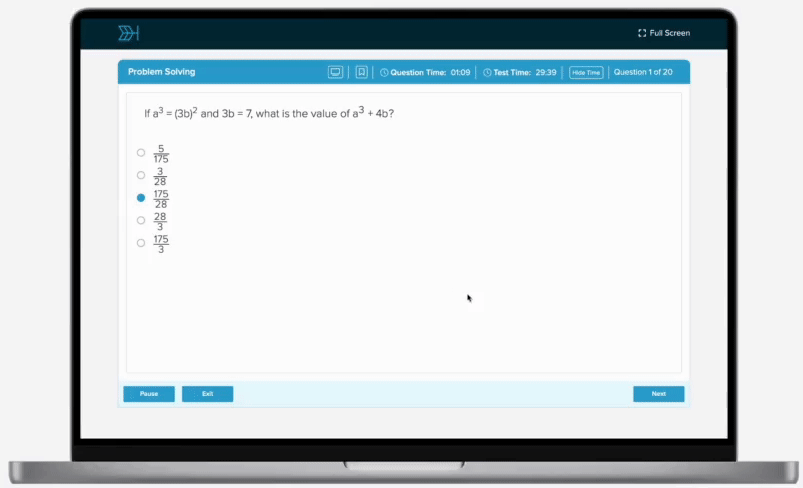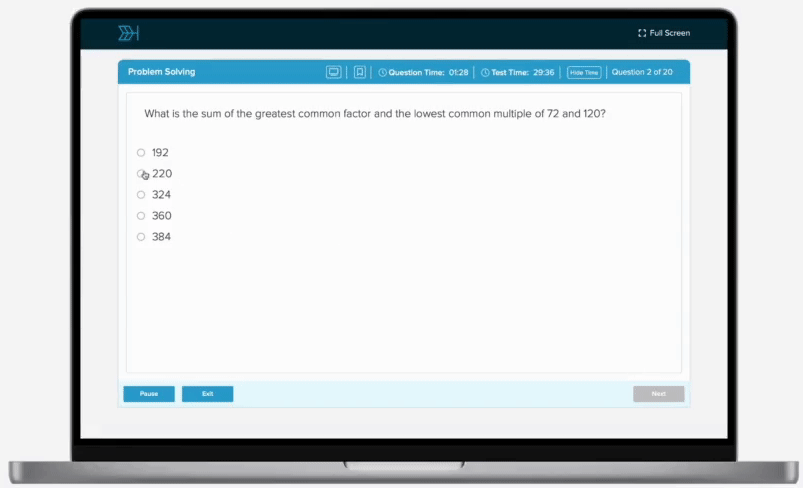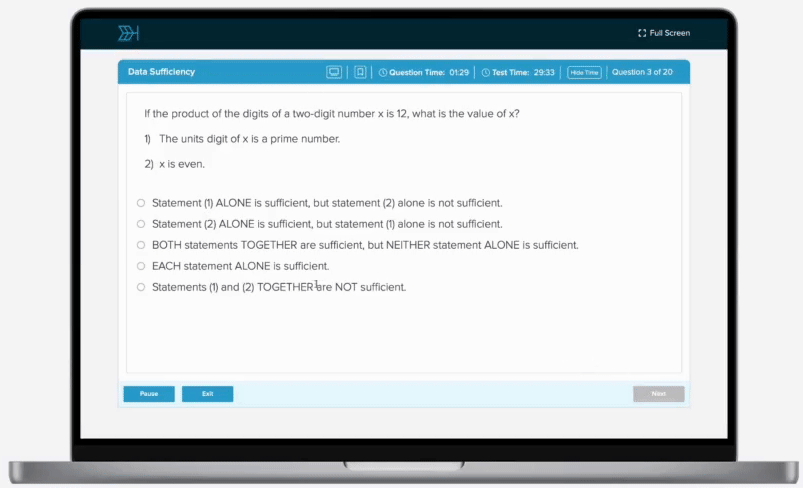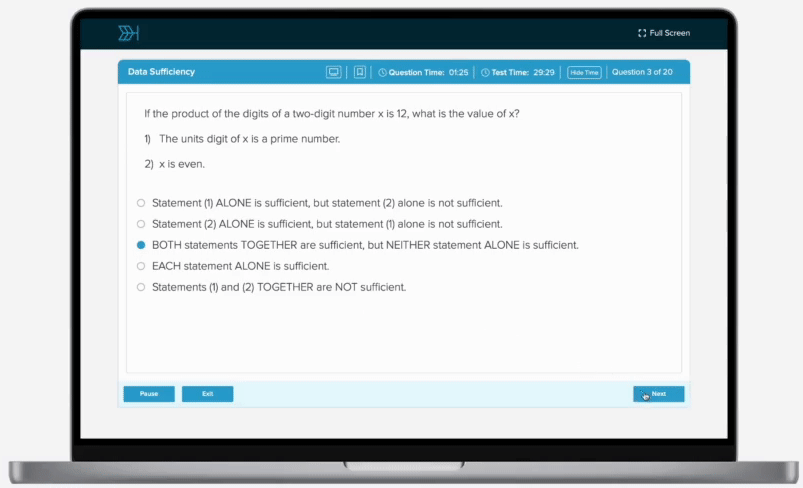
A manager must assign nine out of ten workers to three different teams, namely a design team, a construction team, and a control team. If each team is composed of three workers and no worker is allowed to be on more than one team, in how many different ways can the three teams be formed?
100 × 10
120 × 20
130 × 15 × 2
140 × 20 × 4
120 × 35 × 4
 Scott Woodbury-Stewart
Founder and Expert GMAT Instructor
Scott Woodbury-Stewart
Founder and Expert GMAT Instructor

Text Solution:
The best approach to this problem is to systematically analyze the possible combinations for each team. The manager must assign three workers to the design team, so using the box and fill method, we’ll make three boxes. Since she chooses these workers from among the ten workers at her disposal, place a ten in box one.
She now has nine workers from whom to choose. Place a nine in box two.
She now has eight workers from whom to choose. Place an eight in box three.
Because this is a combination, divide the product of the boxes by the factorial of the number of boxes.
Thus, there are 120 possible ways to select the design team. Let’s now consider what’s different about the construction team. She must still choose three workers for the construction team, but since three workers were already assigned to the design team, only seven workers remain from whom to select. The box and fill diagram for the construction team would be as follows:
She must also assign three workers to the control team, but she has already assigned six of the ten available workers. Thus, only four workers remain in the pool.
Therefore, there are 120 × 35 × 4 = 16,800 possible team configurations.