Scott Woodbury-Stewart
Founder and Expert GMAT Instructor
Scott Woodbury-Stewart
Founder and Expert GMAT Instructor

Text Solution:
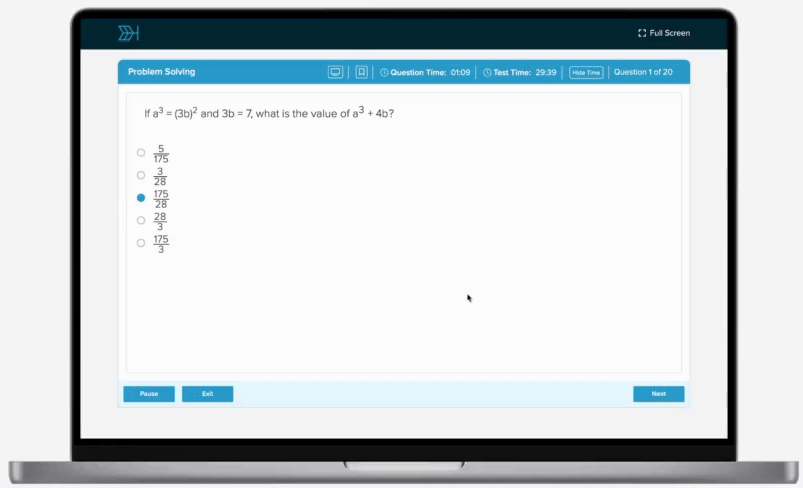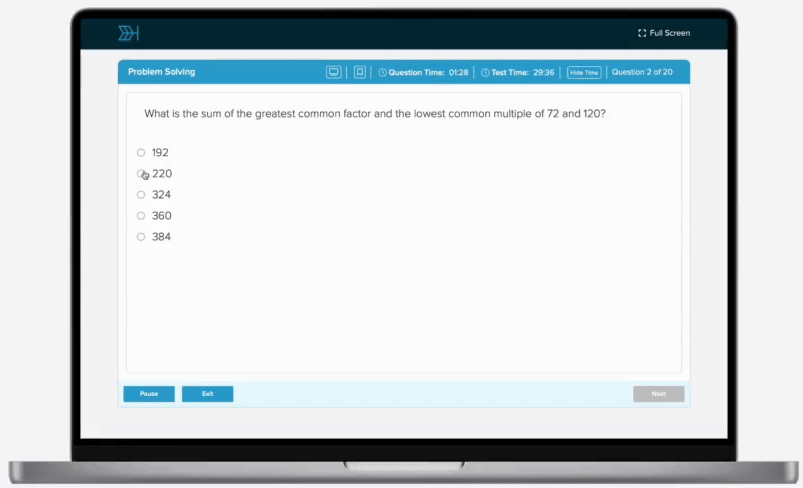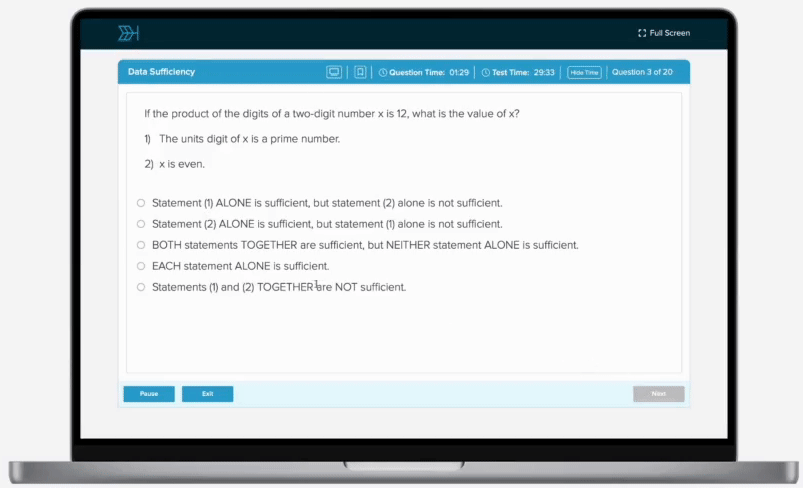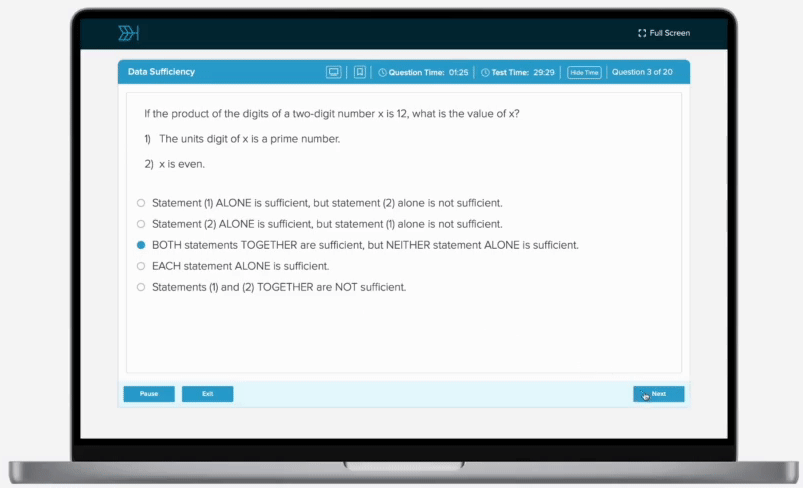
Since 54 is the highest power of the base 5, the LCD must be 54. Let’s convert each fraction to the common denominator of 54, so that we can combine them. Because we see that each answer choice has an integer with no exponents in its numerator, we will simplify any exponents in the numerator in our work, but leave the exponent in the denominator as it is: