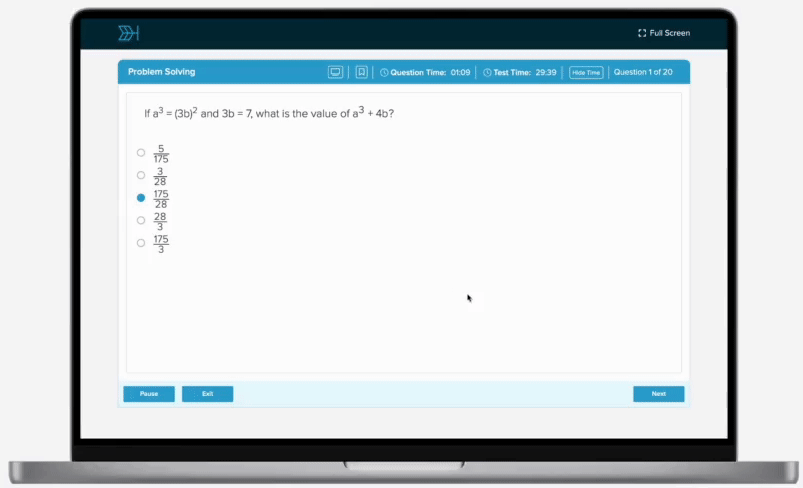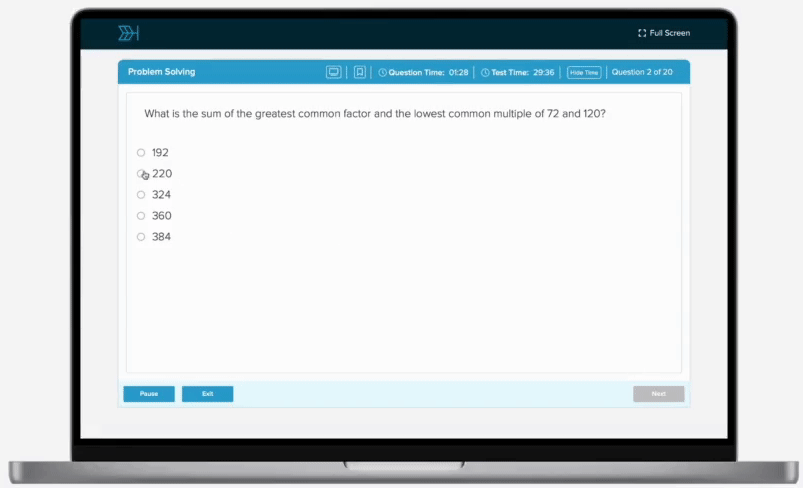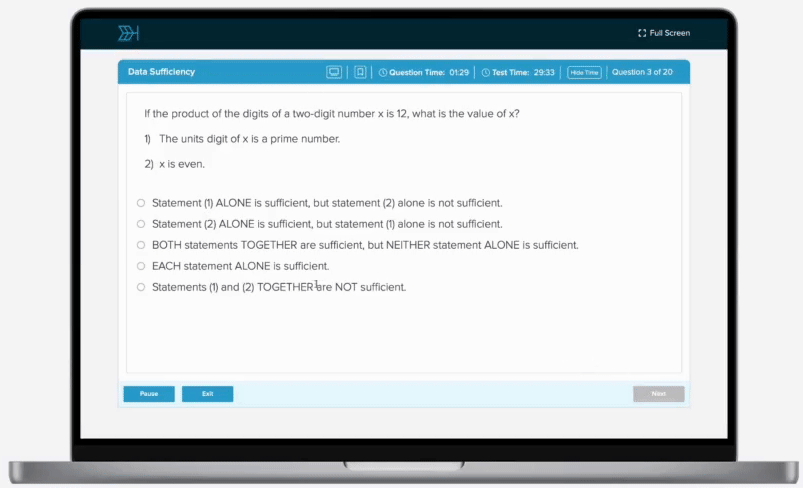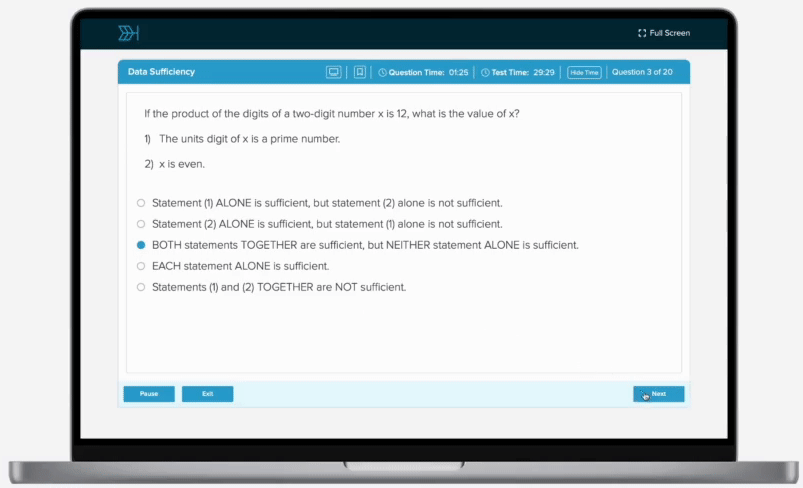
The volume of a pyramid varies directly jointly with its height and the area of its base. A pyramid with a height of 12 feet and a base with an area of 23 square feet has a volume of 92 cubic feet. Find the volume, in cubic feet, of a pyramid with a height of 13 feet and a base with an area of 24 square feet.
48
104
192
276
312
 Scott Woodbury-Stewart
Founder and Expert GMAT Instructor
Scott Woodbury-Stewart
Founder and Expert GMAT Instructor

Text Solution:
We can let V, h, and A represent the volume, height, and base area of the pyramid, respectively. Because V varies directly jointly with h and A, we can set up a joint variation equation , where k is some unknown constant. Substituting the initial given values for V, h, and A, we can solve for k.
Now that we know the value of k in a pyramid’s volume equation, we can determine V when h = 13 and A = 24.
The volume of the pyramid is 104 cubic feet.