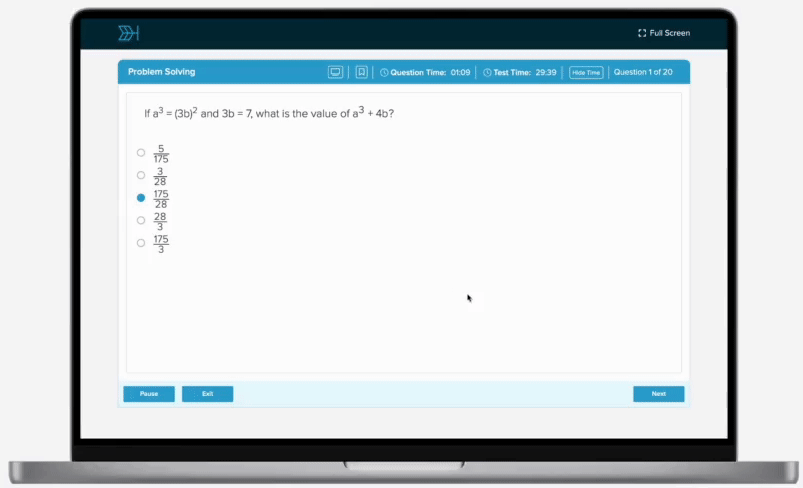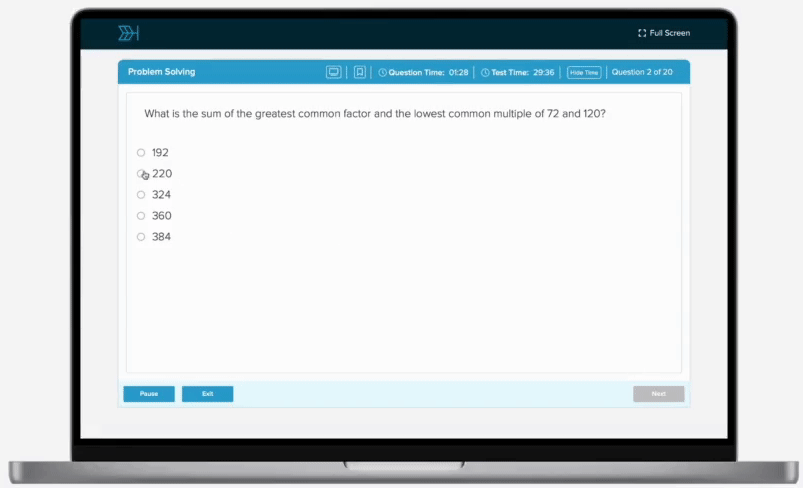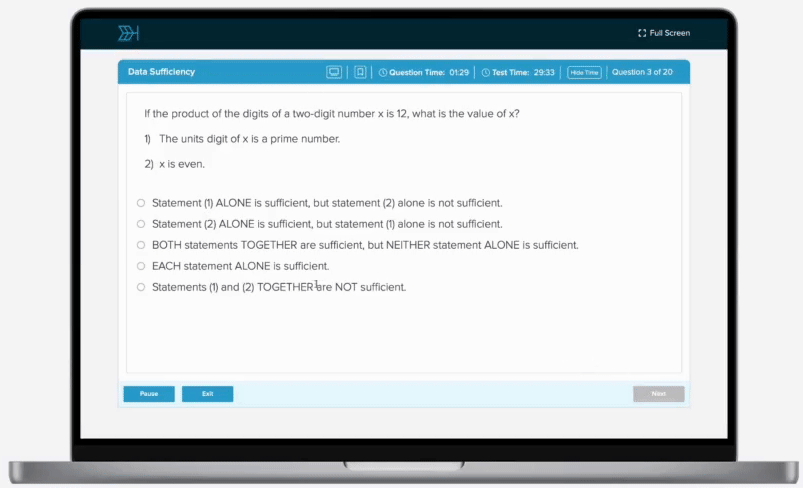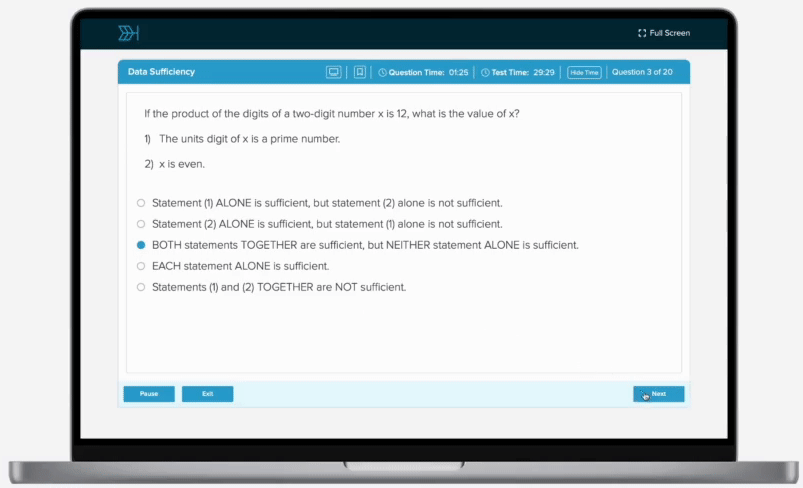
A box contains dark and white chocolate candies. Each type of chocolate candies can be either round or square. There is an probability of selecting a dark chocolate candy, a probability of selecting a round chocolate candy, and a probability of selecting a round and dark chocolate candy. What is the probability that a randomly selected chocolate candy is neither dark nor round?
 Scott Woodbury-Stewart
Founder and Expert GMAT Instructor
Scott Woodbury-Stewart
Founder and Expert GMAT Instructor

Text Solution:
Let’s define A as chocolate is dark and B as chocolate is round. Using the above formula, we have:
P(A) =
P(B) =
We are told that the probability of selecting a round and dark chocolate candy is :
P(both A and B) =
1 = P(A) + P(B) - P(both A and B) + P(neither A nor B)
1 =
1 =
1 =
Therefore, the probability that a randomly selected chocolate is neither dark nor round is .