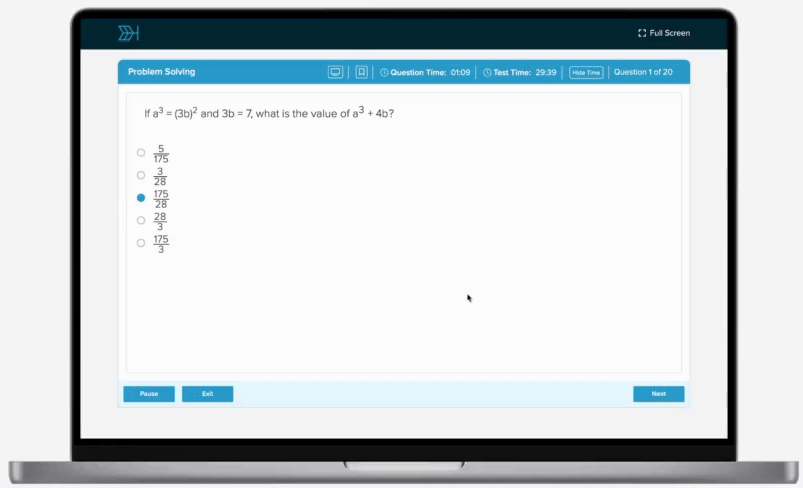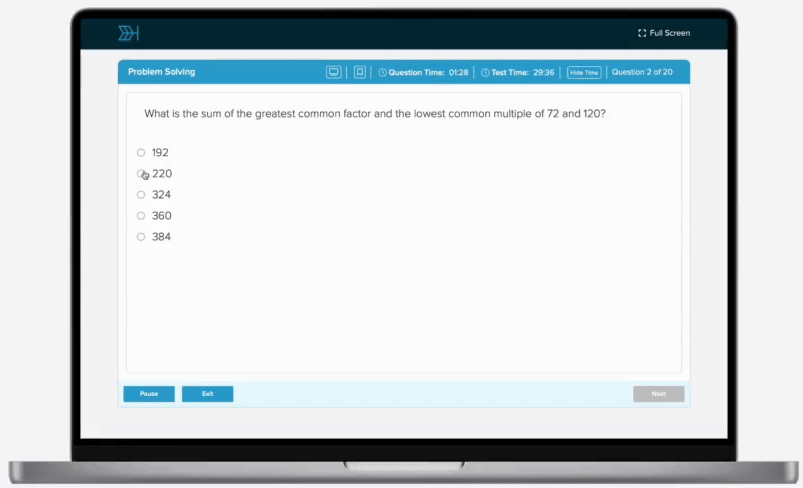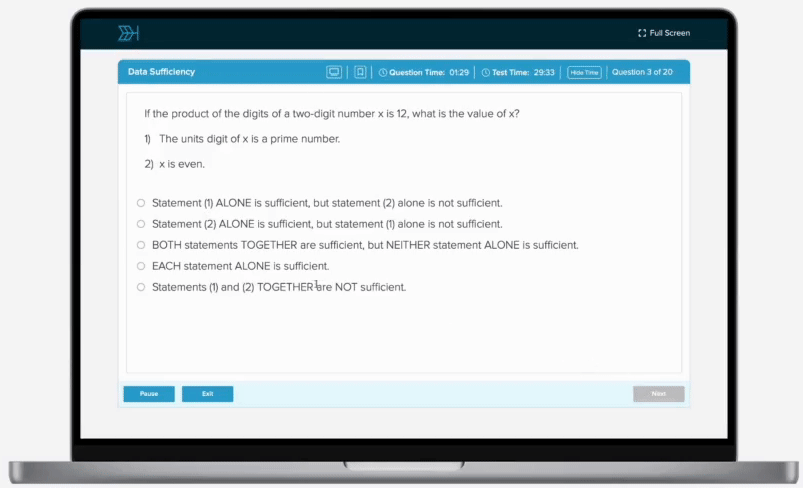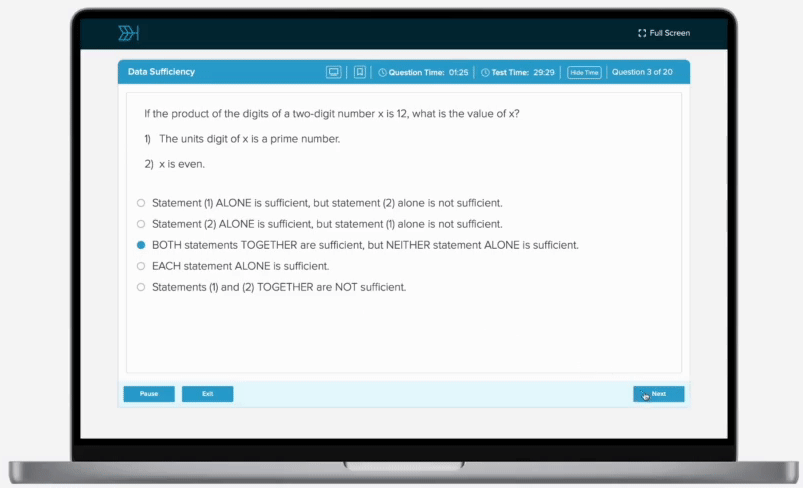
If 6 identical machines, each working at the same uniform constant rate, can complete a job working together in 3 hours, how long will it take 9 of these machines, working at their constant rate, to complete of this job?
60 minutes
45 minutes
40 minutes
30 minutes
24 minutes
 Scott Woodbury-Stewart
Founder and Expert GMAT Instructor
Scott Woodbury-Stewart
Founder and Expert GMAT Instructor

Text Solution:
Let’s start by determining the rate of one machine.
First, we need to determine the rate of 6 machines:
.
Next, we can determine the rate of 1 machine. To do so, we divide the rate of the 6 machines by 6:
Finally, we need to determine the rate of 9 machines, so we multiply the rate of one machine by 9:
.
Keep in mind, we also could have used the proportion method:
Now that we have the rate of 9 machines, we see that we need to determine how long it will take the 9 machines to complete of the job, so we can put this into a matrix.
| Rate | Time | Work | |
|---|---|---|---|
| 9 Machines | job hour | ? | job |
Since we have the following: