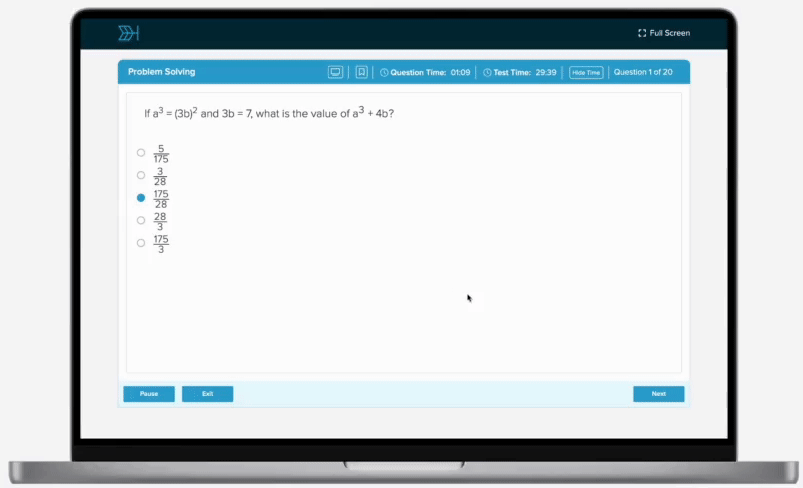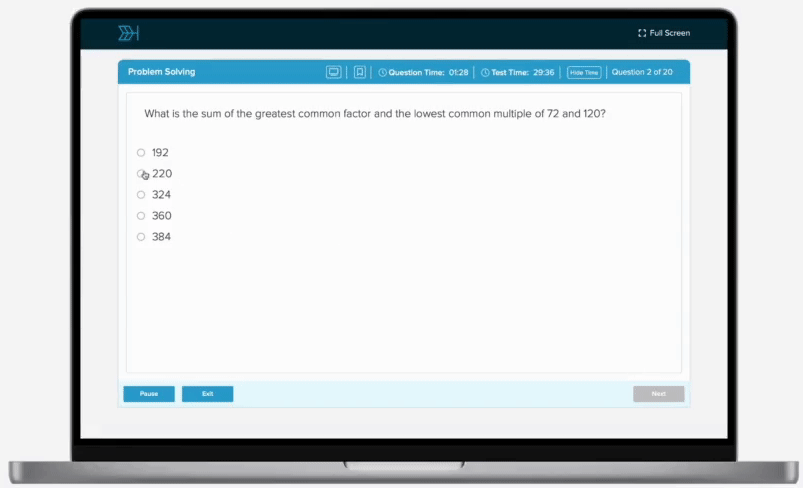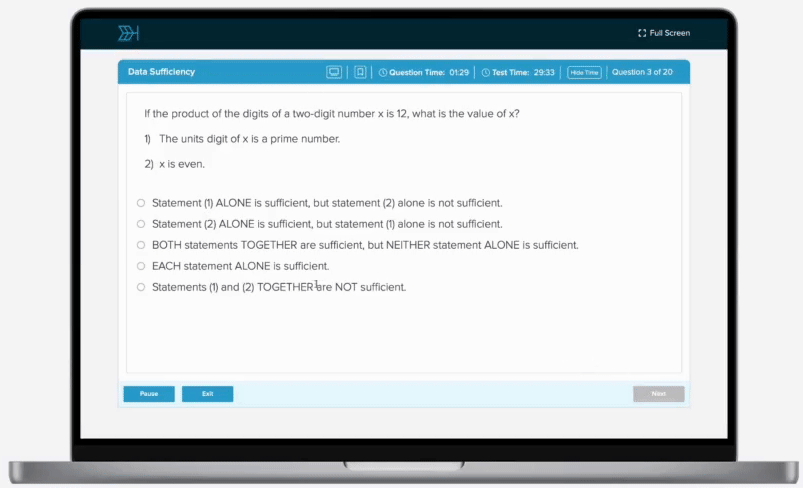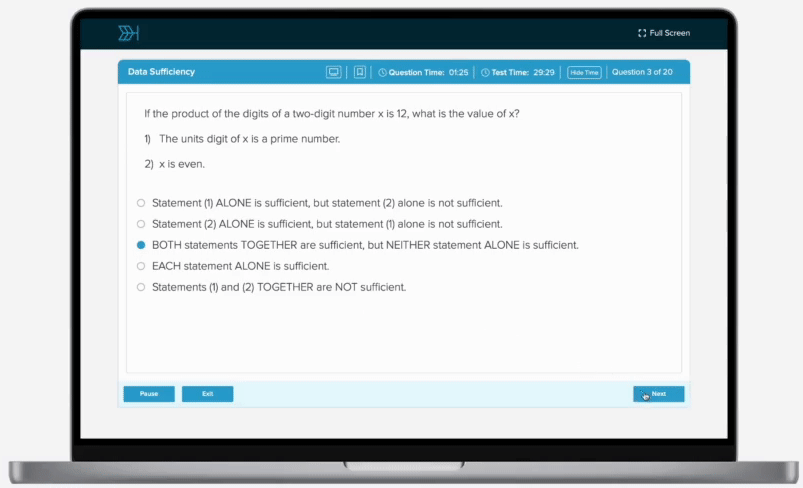
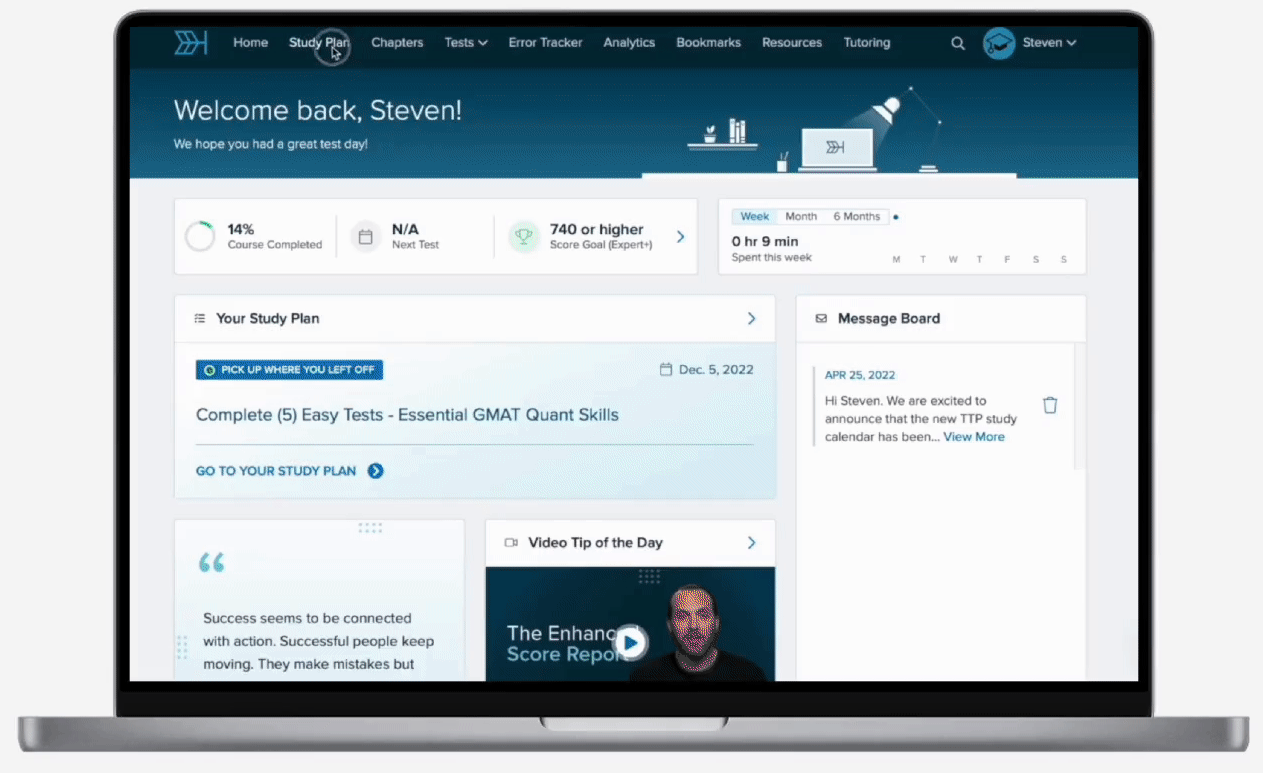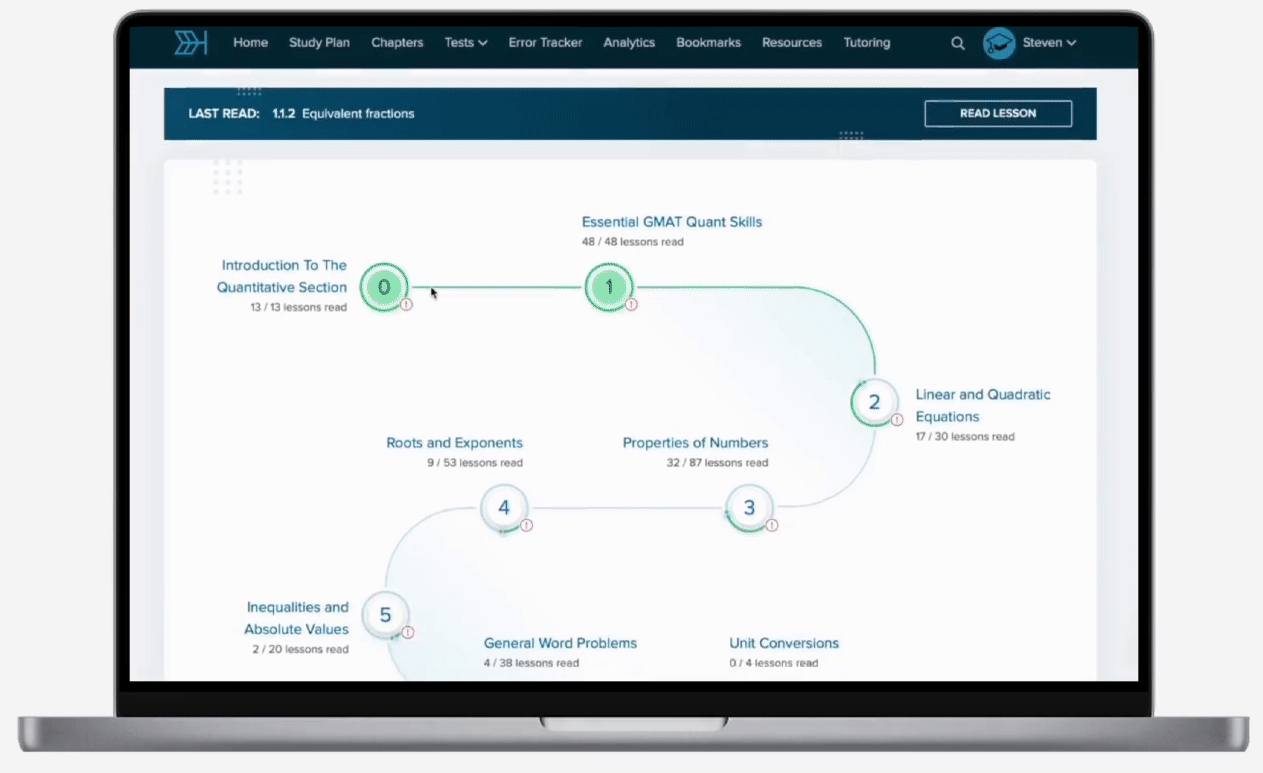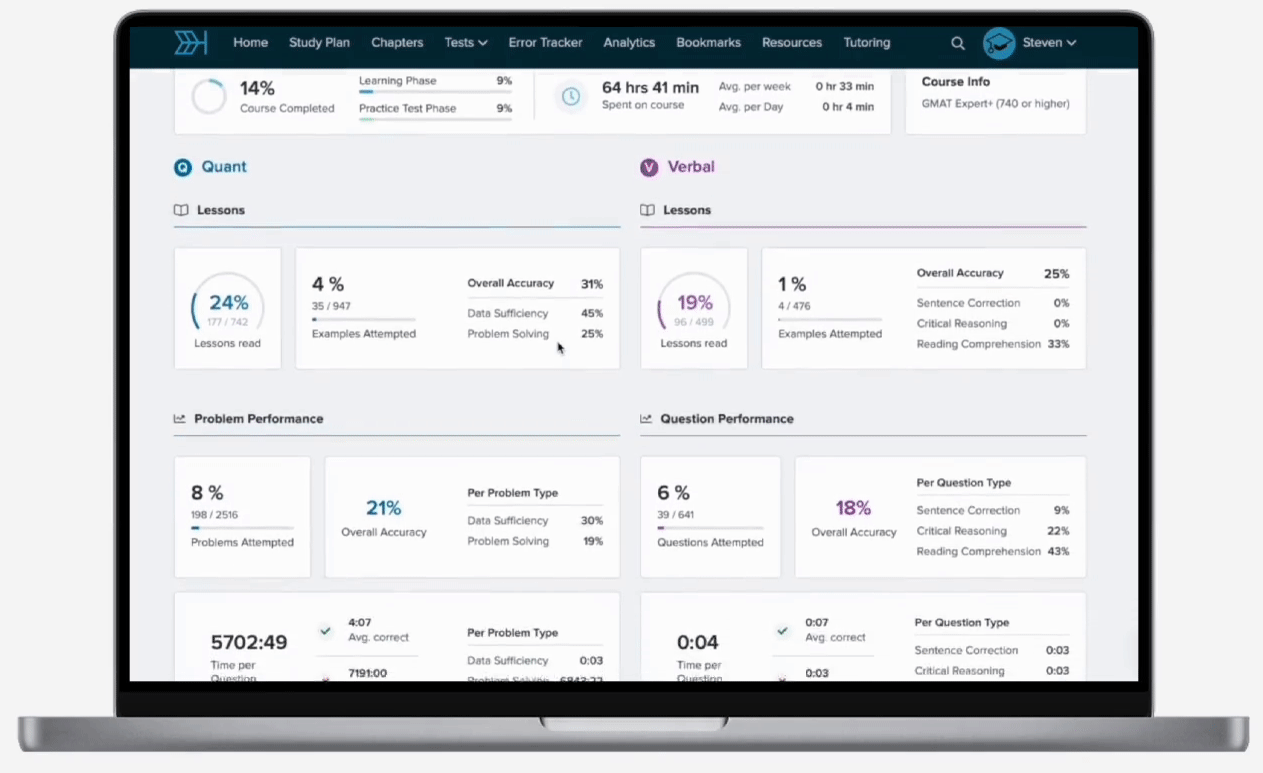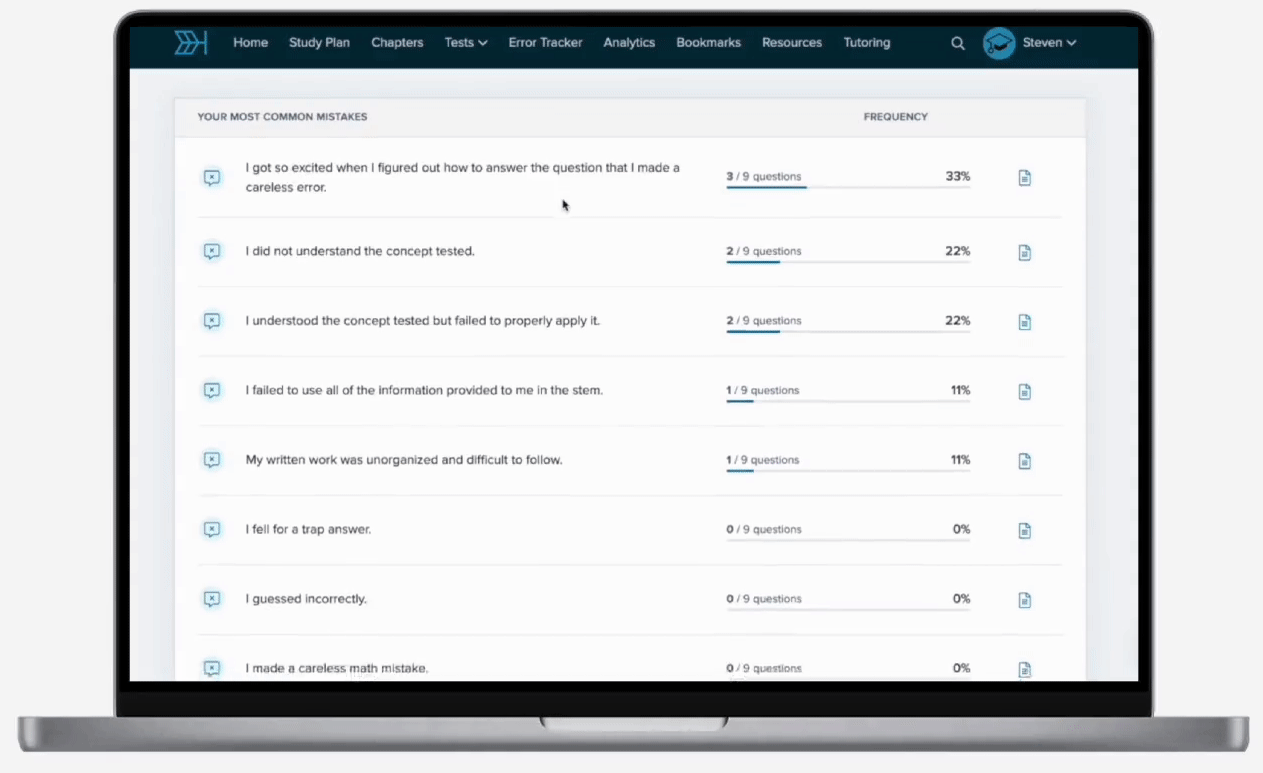
Catherine’s cat, Edward, spent his Saturday eating cat treats. Edward ate of his treats after breakfast, of the remaining treats after lunch, and 21 of the treats for an afternoon snack. If Edward then had 12 treats remaining, how many treats did he originally have?
57
66
70
73
84
 Scott Woodbury-Stewart
Founder and Expert GMAT Instructor
Scott Woodbury-Stewart
Founder and Expert GMAT Instructor

Text Solution:
We can let T = the original number of treats and use the following formula:
fractional part 1 + fractional part 2 + part 3 + remaining part = T
treats after breakfast + treats after lunch + treats for snack + remaining treats = T
Let’s now determine fractional parts 1 and 2.
Since Edward ate of his treats after breakfast, we have the following:
We note that, since he has eaten , there are treats remaining.
Since Edward ate of the remaining treats after lunch, he ate of the treats remaining. Thus:
is the number of treats he ate after lunch.
Lastly, we are given that he ate 21 treats for his afternoon snack, and then 12 treats remained. We can substitute this information into the original formula:
Multiplying the entire equation by 6 to clear the fractions, we have the following: