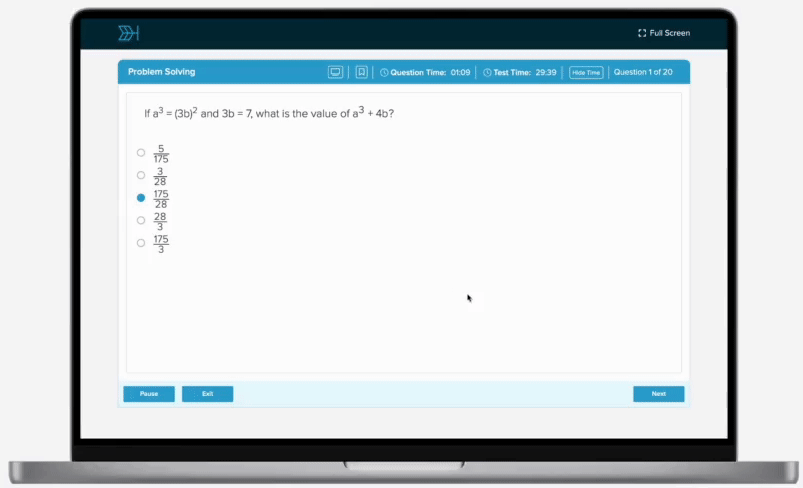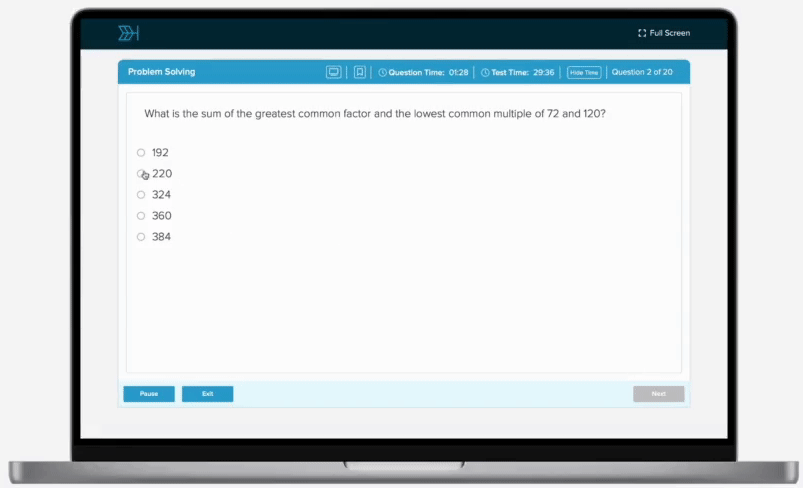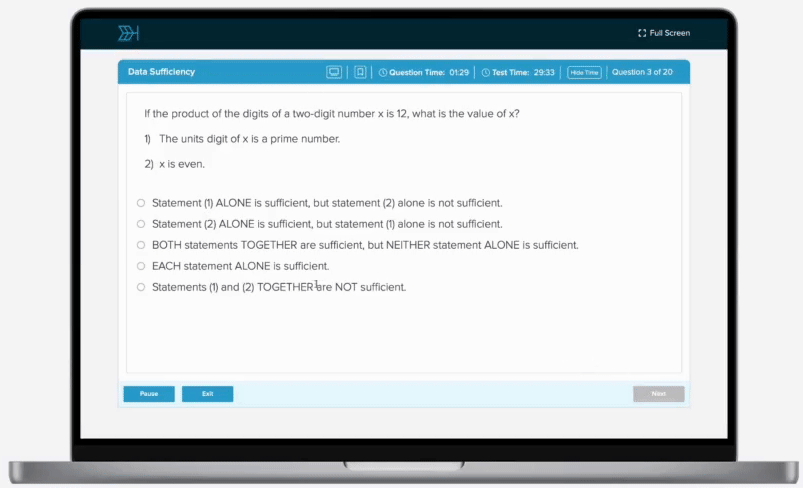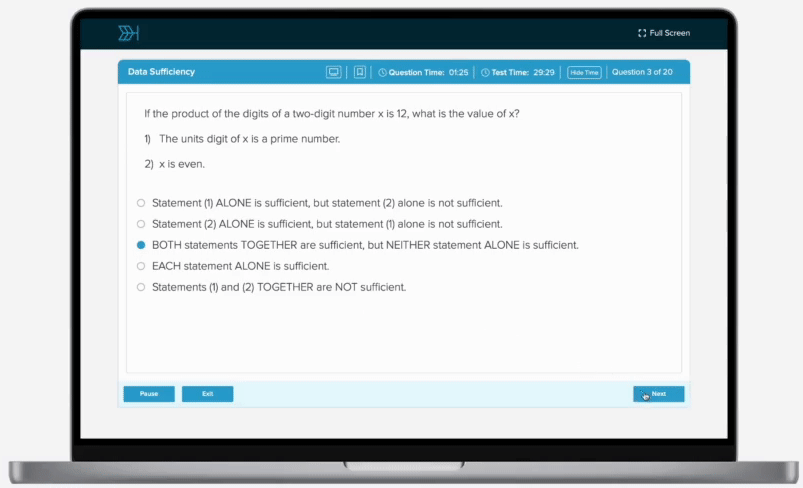
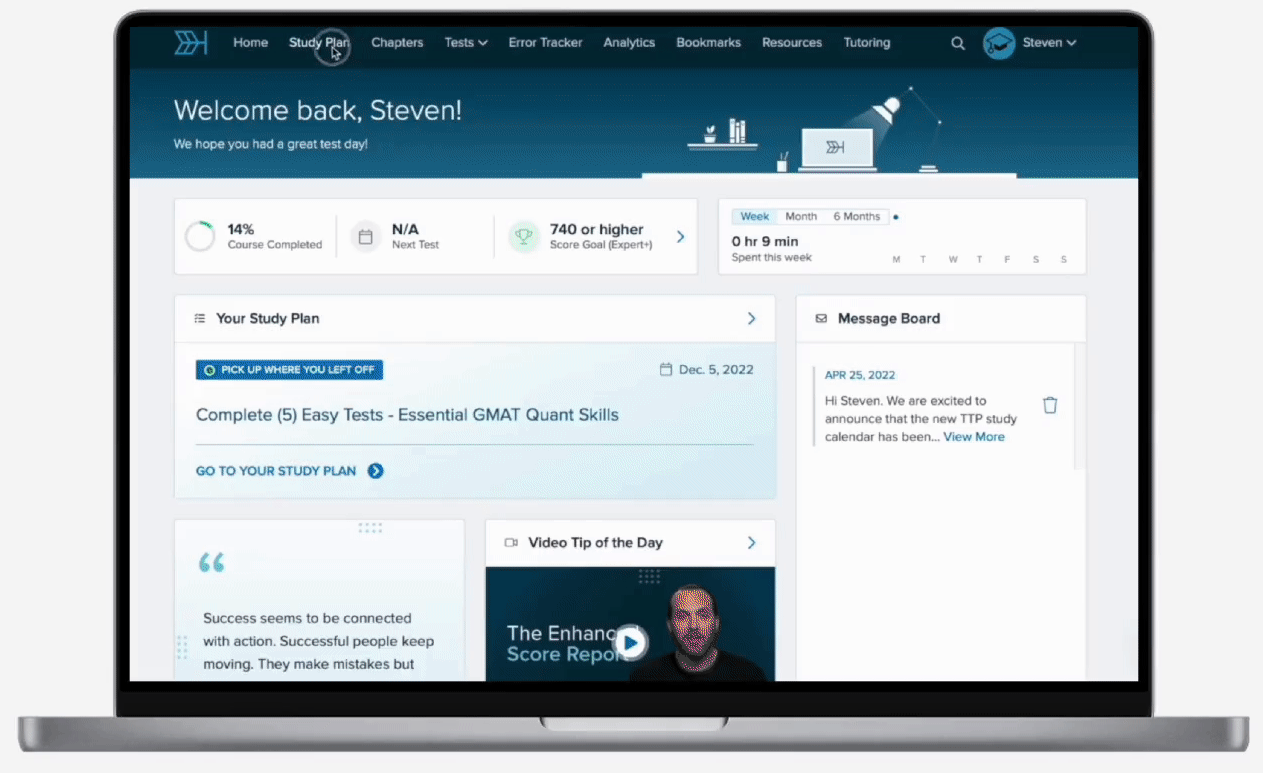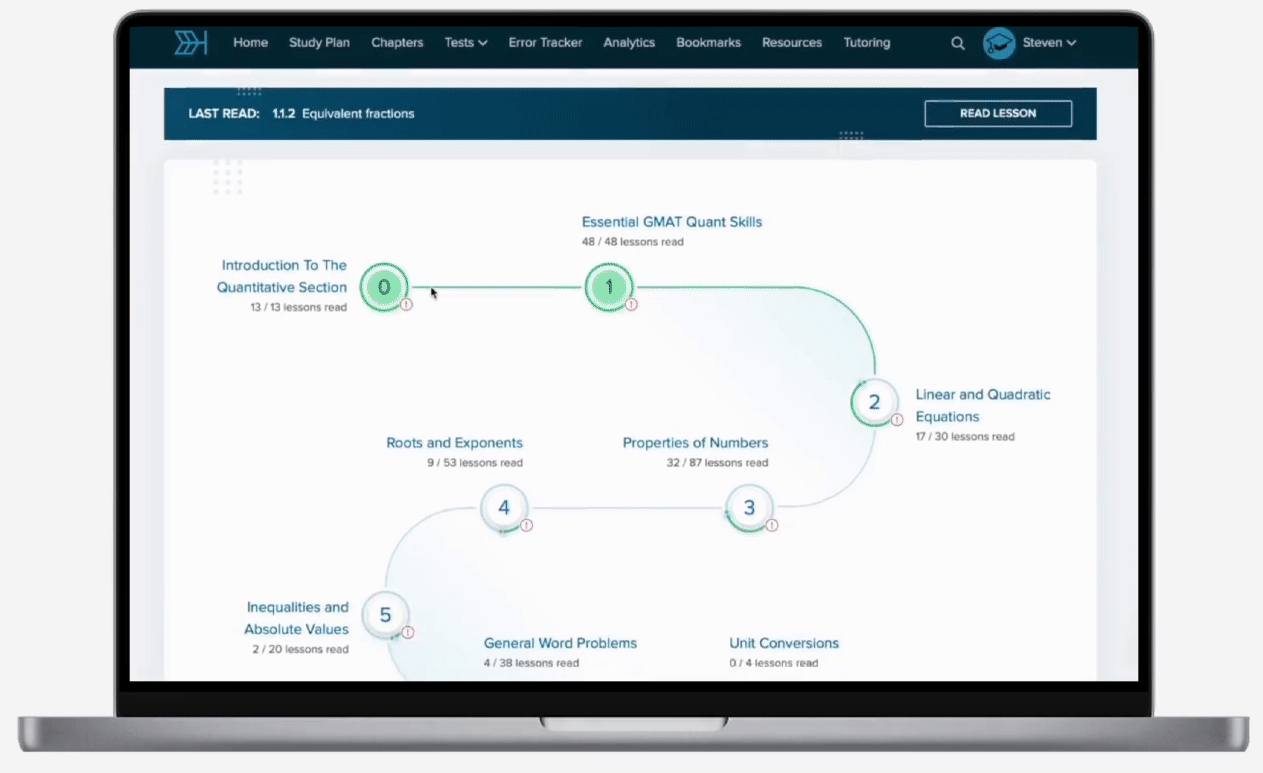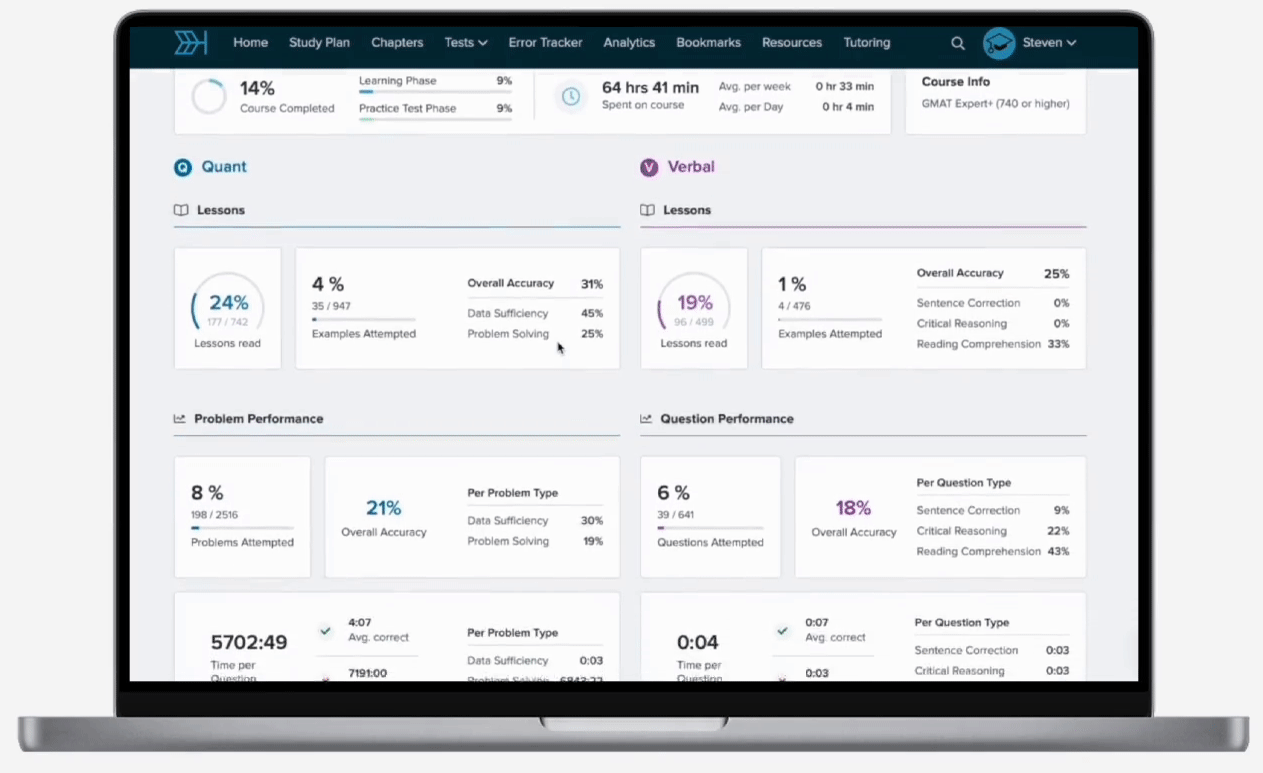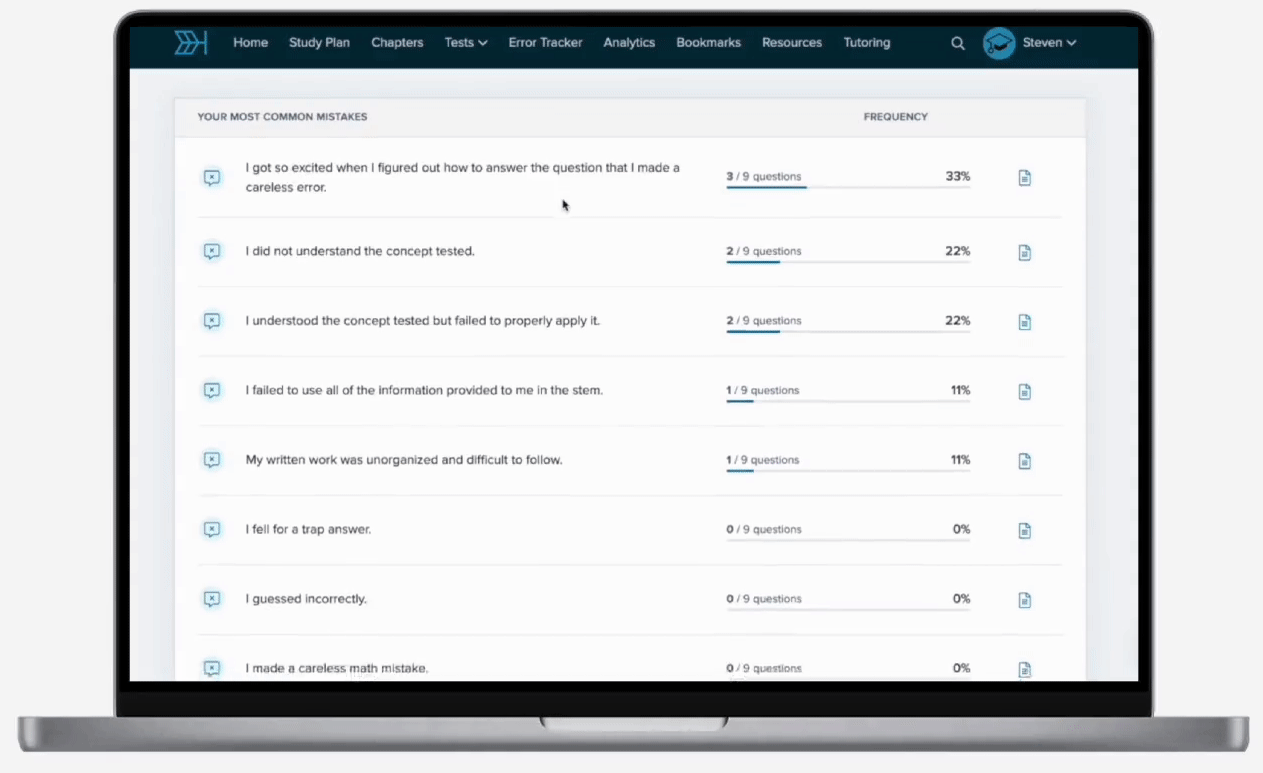
If and , what is the value of y?
0
 Scott Woodbury-Stewart
Founder and Expert GMAT Instructor
Scott Woodbury-Stewart
Founder and Expert GMAT Instructor

Text Solution:
While this is a system of two equations, we can apply the same strategy of clearing the fractions from each equation using the LCM. The first equation has denominators of 3 and 2. The multiples of 3 are 3, 6, …. The multiples of 2 are 2, 4, 6, …. Thus, we see that the LCM of 3 and 2 is 6. We can multiply the entire first equation by 6 and simplify:
For the second equation, we see that the LCM of the denominators is the sole denominator, which is 5. Thus, we multiply the entire equation by 5 and simplify:
To determine the value of y, we can solve the system of equations by using the substitution method. In order to do so, let’s isolate x in the second equation by adding 10y to both sides:
We can now substitute 10y + 15 for x in the first equation: